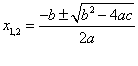על מנת לערוך סיכומים נדרש לפתוח חשבון.
נוסחת השורשים: הבדלים בין גרסאות בדף
קפיצה לניווט
קפיצה לחיפוש
(כדאי להוסיף עוד דוגמאות) |
אין תקציר עריכה |
||
| שורה 2: | שורה 2: | ||
נוסחת השורשים היא נוסחה למציאת נעלם X במשוואה ממעלה שניה מהצורה: [[Image:Ax^2-bx-c=0 sldkhf.png]] כאשר [[Image:Ax^2-bx-c=0 תנאי.png]].<BR> | נוסחת השורשים היא נוסחה למציאת נעלם X במשוואה ממעלה שניה מהצורה: [[Image:Ax^2-bx-c=0 sldkhf.png]] כאשר [[Image:Ax^2-bx-c=0 תנאי.png]].<BR> | ||
כדי למצוא את שורשי המשוואה (כלומר את הפתרונות) נציב את המקדמים a, b, c בנוסחת השורשים: [[Image:Nuschanshorashim.gif]]<BR> | כדי למצוא את שורשי המשוואה (כלומר את הפתרונות) נציב את המקדמים a, b, c בנוסחת השורשים: [[Image:Nuschanshorashim.gif]]<BR> | ||
ייתכנו שלושה מצבים: שני פתרונות, פתרון אחד ואפס פתרונות. | ייתכנו שלושה מצבים: שני פתרונות, פתרון אחד ואפס פתרונות.<br> | ||
כאשר a=0 אין להשתמש בנוסחה, והמשוואה אינה ממעלה שנייה. | |||
===דוגמאות=== | ===דוגמאות=== | ||
גרסה מ־06:15, 27 בפברואר 2006
- רמה:כיתה ט' - י"ב.
נוסחת השורשים היא נוסחה למציאת נעלם X במשוואה ממעלה שניה מהצורה: 
כאשר 
.
כדי למצוא את שורשי המשוואה (כלומר את הפתרונות) נציב את המקדמים a, b, c בנוסחת השורשים: 
ייתכנו שלושה מצבים: שני פתרונות, פתרון אחד ואפס פתרונות.
כאשר a=0 אין להשתמש בנוסחה, והמשוואה אינה ממעלה שנייה.
דוגמאות
המקדמים: 
ישנם שני פתרונות: פתרון אחד כשלוקחים את הפלוס ופתרון שני כשלוקחים את המינוס.
