על מנת לערוך סיכומים נדרש לפתוח חשבון.
נוסחת השורשים: הבדלים בין גרסאות בדף
קפיצה לניווט
קפיצה לחיפוש
אין תקציר עריכה |
אין תקציר עריכה |
||
| שורה 5: | שורה 5: | ||
כאשר a=0 אין להשתמש בנוסחה, והמשוואה אינה ממעלה שנייה. | כאשר a=0 אין להשתמש בנוסחה, והמשוואה אינה ממעלה שנייה. | ||
* הביטוי בתוך השורש b<sup>2</sup>-4ac נקרא דסקרימיננטה והיא מסומנת באות הגדולה היוונית דלתא. ניתן לקבוע את מספר הפתרונות של משוואה ריבועית על פי ערך הדסקימיננטה: | * הביטוי בתוך השורש b<sup>2</sup>-4ac נקרא דסקרימיננטה והיא מסומנת באות הגדולה היוונית דלתא - Δ. ניתן לקבוע את מספר הפתרונות של משוואה ריבועית על פי ערך הדסקימיננטה: | ||
** '''דיסקרימיננטה קטנה מאפס''' - אין פתרונות. | ** '''דיסקרימיננטה קטנה מאפס''' - אין פתרונות. | ||
** '''דיסקרימיננטה שווה לאפס''' - יש פתרון אחד. | ** '''דיסקרימיננטה שווה לאפס''' - יש פתרון אחד. | ||
גרסה מ־15:52, 27 בפברואר 2006
- רמה:כיתה ט' - י"ב.
נוסחת השורשים היא נוסחה למציאת נעלם X במשוואה ממעלה שניה מהצורה: 
כאשר 
.
כדי למצוא את שורשי המשוואה (כלומר את הפתרונות) נציב את המקדמים a, b, c בנוסחת השורשים: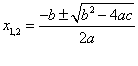 
ייתכנו שלושה מצבים: שני פתרונות, פתרון אחד ואפס פתרונות.
כאשר a=0 אין להשתמש בנוסחה, והמשוואה אינה ממעלה שנייה.
- הביטוי בתוך השורש b2-4ac נקרא דסקרימיננטה והיא מסומנת באות הגדולה היוונית דלתא - Δ. ניתן לקבוע את מספר הפתרונות של משוואה ריבועית על פי ערך הדסקימיננטה:
- דיסקרימיננטה קטנה מאפס - אין פתרונות.
- דיסקרימיננטה שווה לאפס - יש פתרון אחד.
- דיסקרימיננטה חיובית - שני פתרונות שונים.
דוגמאות
המקדמים: 
ישנם שני פתרונות: פתרון אחד כשלוקחים את הפלוס ופתרון שני כשלוקחים את המינוס.
