על מנת לערוך סיכומים נדרש לפתוח חשבון.
נוסחת השורשים: הבדלים בין גרסאות בדף
קפיצה לניווט
קפיצה לחיפוש
אין תקציר עריכה |
אין תקציר עריכה |
||
| שורה 11: | שורה 11: | ||
כדי למצוא את שורשי המשוואה (כלומר את הפתרונות) נציב את המקדמים a, b, c בנוסחת השורשים: [[Image:Nuschanshorashim.gif]]<BR> | כדי למצוא את שורשי המשוואה (כלומר את הפתרונות) נציב את המקדמים a, b, c בנוסחת השורשים: [[Image:Nuschanshorashim.gif]]<BR> | ||
ייתכנו שלושה מצבים: שני פתרונות, פתרון אחד ואפס פתרונות. | ייתכנו שלושה מצבים: שני פתרונות, פתרון אחד ואפס פתרונות. | ||
===דוגמאות=== | ===דוגמאות=== | ||
<div align=left> | |||
[[Image:נוסחת השורשים ד1ת1ט1.png]]<br> | |||
המקדמים: [[Image:נוסחת השורשים ד1ת2ט1.png]]<br> | |||
[[Image:נוסחת השורשים ד1ת3ט1.png]]<br> | |||
</div> | |||
גרסה מ־06:54, 27 בפברואר 2006
- רמה:כיתה ט' - י"ב.
סיכום זה נמצא בעריכה. אתם מתבקשים לא לערוך אותו עד שתוסר ההודעה |
| מותר לערוך את הסיכום אם העורך ששם את ההודעה לא ערך את הסיכום בשבוע האחרון |
נוסחת השורשים היא נוסחה למציאת נעלם X במשוואה ממעלה שניה מהצורה: ![]() כאשר
כאשר ![]() .
.
כדי למצוא את שורשי המשוואה (כלומר את הפתרונות) נציב את המקדמים a, b, c בנוסחת השורשים: 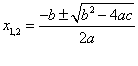
ייתכנו שלושה מצבים: שני פתרונות, פתרון אחד ואפס פתרונות.
דוגמאות
- כעת ישנן שתי אפשרויות(כפי שניתן לראות לפי הנוסחה קיימת אפשרות של חיבור או חיסור של תוצאת השורש במשוואה),חיבור\חיסור תוצאת השורש במשוואה:
