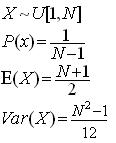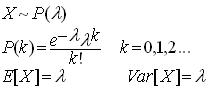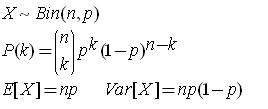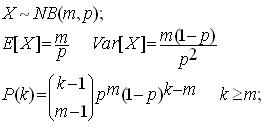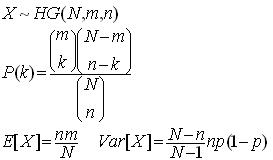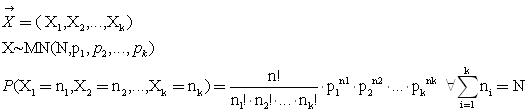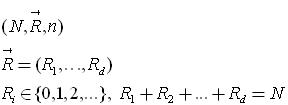על מנת לערוך סיכומים נדרש לפתוח חשבון.
התפלגויות: הבדלים בין גרסאות בדף
אין תקציר עריכה |
אין תקציר עריכה |
||
| (3 גרסאות ביניים של 2 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
חזרה ל[[הסתברות]] | |||
---- | |||
==התפלגויות – סיכום== | ==התפלגויות – סיכום== | ||
| שורה 126: | שורה 129: | ||
===התפלגות היפרגיאומטרית הרב מימדית=== | ===התפלגות היפרגיאומטרית הרב מימדית=== | ||
נאמר שהוקטור[[Image: | נאמר שהוקטור[[Image:Pilu11.JPG]] מפולג היפר גיאומטרי עם הפרמטרים: | ||
[[Image:Pilu12.JPG|left]] | |||
ונסמן[[Image:Pilu13.JPG]] הסבר: | |||
יש אוכלוסיה של N אנשים. | |||
Ri אנשים מצביעים עבור מפלגה i כאשר R1+R2+…+Rd=N. | |||
לוקחים מדגם של n אנשים. | |||
אז Xi הוא מספר הבוחרים של מפלגה i שהתקבל במדגם. | |||
[[Category:מתמטיקה]] | |||
גרסה אחרונה מ־15:56, 28 ביוני 2006
חזרה להסתברות
התפלגויות – סיכום
1התפלגות אחידה – יוניפורמית
X הוא מ"מ מפולג אחיד על הקטע [1,N] אם הוא מציין נקודה שנבחרה באקראי בקטע שבין1 ל N.
ונסמן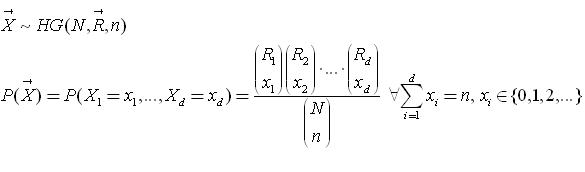
התפלגות פואסון
X משתנה מקרי המקבל את הערכים...,0,1,2 הוא משתנה מקרי פואסוני עם הפרמטר , אם לכל
מתקיים
התפלגות גיאומטרית:
X משתנה מקרי גיאומוטרי עם הפרמטר p אם עורכים ניסויים, הסתברות ההצלחה בכל ניסוי היא P וההסתברות להצלחה ראשונה בנסיון ה- K היא
התפלגות בינומית:
X משתנה מקרי בינומי אם עורכים n ניסויי ברנולי, ההסתברות להצלחה בכל ניסוי היא p וההסתברות לקבל בדיוק k הצלחות היא:
התפלגות בינומית שלילית:
X משתנה מקרי בינומי שלילי אם עורכים ניסויים בלתי תלויים, ההסתברות להצלחה בכל ניסוי היא p וההסתברות לקבל את m הצלחות בk ניסויים:
התפלגות היפרגיאומטרית:
בוחרים באקראי (ובלי החזרה) מדגם בגודל n, מתוך כד המכיל N כדורים מתוכם m לבנים והשאר שחורים. X מ"מ היפרגיאומטרי מתאר את מספר הכדורים הלבנים שנבחו.
התפלגות מולטינומית
מבצעים N ניסויים בלתי תלויים . לכל ניסוי קיימות k תוצאות אפשריות כך שההסתברות לתוצאה i היא ומתקיים
הוא מספר התוצאות מסוג i שהתקבלו ב-N הניסויים
התפלגות היפרגיאומטרית הרב מימדית
נאמר שהוקטור מפולג היפר גיאומטרי עם הפרמטרים:
ונסמן